数组之纠结的排序
1.数组是什么?
- 数组:所谓数组,就是相同数据类型的元素按一定顺序排列的集合,就是把有限个类型相同的变量用一个名字命名,然后用编号区分他们的变量的集合,这个名字称为数组名,编号称为下标。组成数组的各个变量称为数组的分量,也称为数组的元素,有时也称为下标变量。数组是在程序设计中,为了处理方便, 把具有相同类型的若干变量按有序的形式组织起来的一种形式。这些按序排列的同类数据元素的集合称为数组。
- 数组在之前的画图工具中也有使用到,主要是利用数组来存储数据,实现重绘和添加多个功能和颜色按钮。使用的比较多的是一维数组和二维数组;一维数组比较好理解,而二维数组就好像是多个一维数组的集合。例如:a[i][j],则可以看做是有i个一维数组,每个一维数组下面又有j个元数;也可以理解为一个表格:i表示行,j表示在每一行下面的列。
2.数组的基本用法:
- 数组的定义:要定义一个数组,就必须要给定数组的长度;数组的定义方式有几种:
- 直接在定义的时候就给数据:
数据类型 [] 数组名 = {数据,...}; 例如: int[] a = { 6, 7, 9, 3, 2, 1, 8, 4, 5, 10 } 二维数组:数据类型 [][] 数组名 = { {数据,...},...};
- 定义的时候给数组的长度,没有具体的数据:数据类型 [] 数组名 = new 数据类型[长度]; 二维数组 :数据类型 [][] 数组名 = new 数据类型[行数][列数] ; 例如:public Shape[] Sh = new Shape[10000];
- 数组的使用:数组是属于Java的引用类型(对象类型)。也就是说,你定义一个数组,也就是相对于定义了一个对象;而数组又和其他的对象有区别;数组对象只有一个唯一的属性length,用来表示数组对象能存储的数据总数。
- 一维数组:数组名.length
- 二维数组:行的长度:数组名.length
- 二维数组:列的长度:数组名[i].length
- 二维数组:所有的元素总数:行的长度(数组名.length)*列的长度(数组名[i].length)这是当列的长度相等的情况; 不相等时,只能是所有的列的长度相加:数组名[行下标].length+...
2.数组的排序:
1.冒泡排序:
- 冒泡排序算法的运作如下:
- 有n个数进行排序,则要进行n-1次循环;
- 每次循环都从数组的第一个数开始循环,每次循环都会把一个最大的数浮上来
- 在每次的循环中都要进行相同的步骤: 相连的数之间进行比较,如果前一个数大于后一个数,则交换,然后接着和下一个数进行比较,同样如果大于下一个数的话,就把它往后放,直到最后一个数;
- 程序代码:
public int[] maopaopaixu(int j) { for (int i = 0; i < a.length - 1; i++) { int c = a[i]; int z = i; z++; int x = a[z]; if (c > x) { a[i] = x; a[z] = c; } } j++; if (j < a.length) return maopaopaixu(j); return a; }
2.快速排序:
- 快速排序(Quicksort)是对冒泡排序的一种改进。基本思想是,通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
- 快排写的有些纠结。之前是确定了一个中点,在排序之前就把数组分成了两部分,但是通过一次排序,最后都没有使其中一部分的所有数据都比另外一部分的所有数据都要小;中点前面会有比它大的数或者是后面有比它小的数;
- 学到的思路是:一趟循环:以第一个数作为比较的点,从数组的两边right,left,分别来就比较,先从数组的右边(数组的末尾)right开始往前找,找到一个比他小,放在当前left的位置,然后在改变left的值,开始在左边往后找,找一个比他大的数,放在left的位置。直到分成了两边,在left=right的时候停止,把作为比较的那个点的值放在left=right的这个值;如图:

- 代码:
public void quicksort(int n[], int left, int right) { int dp;// 中间值; if (left < right) { dp = partition(n, left, right);// 将数组分为两部分,dp前面的数为小于dp的数,dp后面为大于dp的数; quicksort(n, left, dp - 1);// 将数组的前部分进行排序, quicksort(n, dp + 1, right); // 将数组的后部分进行排序 } // 整个递归直到left不小于right的时候结束; } public int partition(int n[], int left, int right) { int pivot = n[left]; // 整个循环直到left不小于right的时候结束; while (left < right) { while (left < right && n[right] >= pivot) right--;// 目的是找到一个比pivot小的数; if (left < right) n[left++] = n[right]; /* * 把n[right]的值赋给当前right的位置, 然后在left++; * n[left] = n[right]; left++; */ while (left < right && n[left] <= pivot) left++; if (left < right) n[right--] = n[left]; /* * 把当前的left的值赋给n[right]之后再right--; * n[right] = n[left]; right--; */ } n[left] = pivot;// 移动pivot的位置;在循环后会有一个位置是多的,这时要把pivot放在这个位置上; return left; }
3.希尔排序:
- 希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。
- 希尔排序:将无序数组分割为若干个子序列,子序列不是逐段分割的,而是相隔特定的增量的子序列,对各个子序列进行插入排序;
-
增量的选择:在每趟的排序过程都有一个增量,至少满足一个规则 增量关系 d[1] > d[2] > d[3] >..> d[t] = 1
(t趟排序); - 在弄清希尔排序前,我们先来看一下插入排序:插入排序的基本思想是:每步将一个待排序的纪录,按其关键码值的大小插入前面已经排序的文件中适当位置上,直到全部插入完为止。也就是说,插入排序是将新的数排入一个已经排好序的数列中,在这里我们可以从第一个元素开始,把第一个元素作为已经排好的数列,然后下一个数开始插入进来,排好序的之后,在又插入一个数,直到全部插入为止;如图:(j和j-1比较,如果j小于j-1,那么就交换他们的位置,加下划线的表示已经排好的数列)
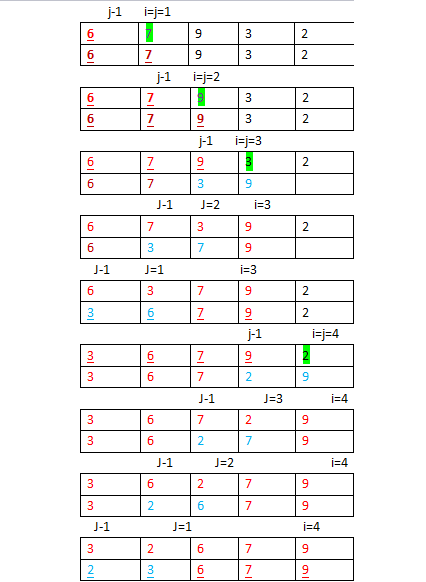
- 希尔排序也是同样的思想,不过他是不连续的把序列分成几个部分,分成相隔特定的增量的子序列,然后在进行插入排序;
- 思路:每一次的循环都先把数列分成2个部分,将后一部分与前一部分进行比较,当后一部分的数大于前一部分的数时,进行交换;
- 如图:(x为增量)(x所在的值与(j-x)所在的位置的值进行比较,当小于时,(j-x)所在的位置的值放到j所在的位置)

- 代码:
public void xierpaixu() { int c = d.length; //分组;选择增量依次为:5,2,1; for (int x = c / 2; x > 0; x /= 2) { //每个组内排序; for (int i = x; i < d.length; i++) { int temp = d[i]; int j = 0; if (temp < d[j - x]) { d[j] = d[j - x]; } else { break; } } d[j] = temp; } } } - 总的来所希尔排序和快排有些相似,可以放在一起比较理解;
4.选择排序:
- 看过快速排序和希尔排序之后,选择排序就比较简单了。
- 选择排序的思路:有n个数,从第一个数开始(i=0),在剩下的数中,找到一个比a[i]小,并且是在比a[i]小的数中是最小的数,然后和a[i]交换坐标。重复相同的步骤,直到序列的最后一个数;
- 选择排序比较简单。这里就不演示了。
3.总结:
- 这次的排序还是做了很长时间的,刚开始的时候是挺着急的,但是沉下来,沉下心来领会,就会发现还是挺有收获的,所以不急不燥,找到自己的速度。